blog…

Quand j’étais à l’école primaire, on m’avait raconté que le Commandant Cousteau avait pu observer, dans sa jeunesse, le Mont Blanc depuis le sommet de la Tour Eiffel lorsque que le temps était parfaitement dégagé. A l’époque, cette information m’avait fasciné comme lorsqu’on m’a dit que la muraille de Chine était visible depuis la Lune.

Autant, j’ai rapidement su que la deuxième affirmation était fausse, autant pour l’observation de Commandant Cousteau, je n’ai jamais vraiment eu la réponse. Alors j’ai décidé de mener ma propre enquête et de déterminer, au moins de manière théorique si cette observation est possible.

Pour mieux comprendre le problème, il faut d’abord rappeler que du sommet de la Tour Eiffel, on se situe à une altitude de 311.2m (276.1m pour la hauteur + 33.5m pour l’altitude au pied de la Tour et 1.60m la hauteur des yeux du Commandant, peut-être surestimée). Le Mont Blanc lui culmine à 4810.4m (même si à l’époque, du commandant Cousteau, tout laisse penser qu’il était légèrement plus petit) et se situe à environ 481.5km de la Tour Eiffel (481.38km d’après Google Earth, 481.93km d’après un calcul prenant en compte l’aplatissement terrestre).

Pour que l’observation soit possible, il faut pouvoir tracer un chemin lumineux entre les deux sommets, sans rencontrer le sol entre les deux. D’ailleurs, pour simplifier les choses, on va supposer qu’il n’y a pas de relief entre les deux.

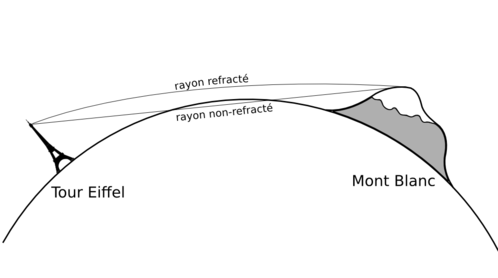
Une autre manière de voir les choses est de chercher à déterminer la distance maximale à laquelle on peut observer depuis une hauteur donnée. Ainsi, si depuis la Tour Eiffel, on voit jusqu’à X km et que depuis le Mont Blanc à Y km alors l’observation est possible si X+Y est supérieure à la distance entre les deux sommets. Sinon, le Mont Blanc est sous l’horizon vu depuis la Tour Eiffel.

En première approximation, le chemin lumineux peut être considéré comme rectiligne et dans ce cas, la distance maximale d’observation peut se calculer facilement: D=√(2*h*R), où h est la hauteur, R le rayon terrestre et D la distance à l’horizon (tous ces paramètres dans les mêmes unités).

Dans la réalité, il faut tenir compte de la réfraction atmosphérique. Celle-ci tend à courber les rayons lumineux et donc à agrandir cette distance à l’horizon. Pour tenir compte de la réfraction, on montre qu’il faut multiplier la précédente relation par un facteur 1/√(1-k) où k est une constante qui dépend de la pression atmosphérique et de la température au sol.

Pour faire le point en mer, les marins prennent habituellement une valeur de k=0.16 (proche de la valeur obtenue pour des conditions standards de pression et température). Avec cette valeur, les distances à l’horizon seront plus grande d’environ 9%. Si maintenant on passe aux applications numériques pour nos deux monuments, on trouve comme distance à l’horizon pour:

• La Tour Eiffel: 68.75km
• Le Mont Blanc: 270.28km

Soit en sommant les deux distances : 339.03km. On est donc loin de la distance entre les deux lieux (481.5km). Le Commandant Cousteau aurait donc mal vu?

Comme je l’ai rappelé, ce facteur k lié à la réfraction dépend de la température et de la pression au niveau du sol. Qu’en est-il si ces deux paramètres varient?

C’est ce que j’ai cherché à savoir. Pour cela, j’ai pris les valeurs extrêmes relevées sur Terre à savoir 870hPa / 1087hPa pour la pression atmosphérique (seulement des valeurs inférieures à 1015hPa impliquent habituellement des nuages donc des conditions d’observations peu favorables) et -89°/+58° pour la température.

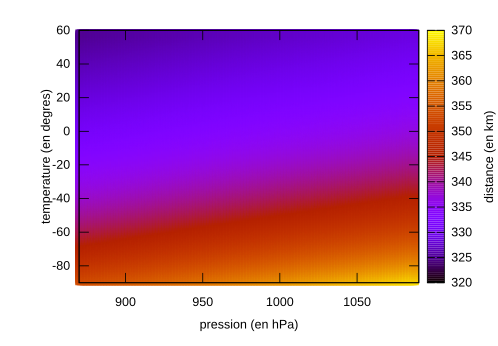
Distance maximale en fonction de la température (°C) et de la pression au sol (hPa).

Comme on le voit, même avec des conditions différentes de pression et de température, on reste encore loin du compte puisqu’il manque encore au moins 110km pour que l’observation soit possible.

En fait, pour que l’observation soit possible dans des conditions atmosphériques normales (à 1015hPa et 10°C), il faudrait que le Mont Blanc fasse plus de 12 500m (pour une Tour Eiffel à sa taille actuelle) ou qu’inversement, la Tour Eiffel fasse au moins 3 140m (pour un Mont Blanc à sa taille actuelle).

Alors quid de l’observation?

• On peut penser que les hypothèses faites pour ce calcul sont trop grossières et ne reflètent pas la réalité. Seulement, les hypothèses sont les mêmes que pour quelques cas d’observations similaires comme l’observation du Mont Canigou depuis les environs de Marseille alors qu’il est théoriquement sous l’horizon.
• Une autre explication reste le mirage atmosphérique. Effectivement possible, mais de là à rallonger la distance à l’horizon théorique de plus 100km, ça parait peu probable.
• Après j’ai peut-être rêvé, et on a affaire à un simple légende urbaine mais reprise tout de même sur quelques sites.
• Mon ultime explication reste qu’il ait pu confondre les sommets enneigés des Alpes avec d’éventuels nuages…

Pour en savoir plus:

Pour ceux qui seraient tenter de trouver leur propre explication, voici quelques liens qui m’ont servi à la rédaction de ce billet:

• La réfraction atmosphérique en montagne de P.Bénard qui propose une bonne approche théorique de la réfraction.
• Le chapitre 9 de l’Astronomie Générale de A.Danjon (sur la réfraction astronomique)
• Enfin différents observations où la réfraction intervient comme l’observation de la Corse depuis les hauteurs de la Côte d’Azur ou le Mont Canigou depuis l’arrière pays marseillais.